
The PSD School
Section 11 by Lars Stenberg, ESDE AB
How to reduce the aberations in the lens systems
In section 10 we studied the shift in the position of the ’light gravity center’ due to the aberrations introduced when we used a simple biconvex lens as main lens. In this section we shall investigate how we can reduce the shift of the light gravity centre by changing the form of the biconvex lens and thereafter investigate what occurs when we use a main lens that comprises more than one lens. The reader is recommended to have at hand section 10 of the PSD school when reading this section.
 For all the examples below the parameters are used which were calculated in section 3 of the PSD school such as the focal length of the main lens being fE = 33,5 mm, DE = 156,649 mm, a = 40° and ß = 5,25°.
For all the examples below the parameters are used which were calculated in section 3 of the PSD school such as the focal length of the main lens being fE = 33,5 mm, DE = 156,649 mm, a = 40° and ß = 5,25°.Figure A shows where the different image field points lie for the image field angles that are used in this section of the PSD school, namely -5,25, -2,625, 0, 2,65 and 5,25 degrees. Figure 2 from section 10 defines what is the chief ray and what are axial rays.
Single lenses
The shift in the position of the ´light gravity centre´ for different lens types is presented with the aid of tables according to the example below that relates to one simple biconvex lens. The spot radii that are specified relate to the radius of the smallest circle that covers the spot diagram and has the chief ray as reference. It is always true that this radius is greater than the radius of the smallest circle that covers the spot diagram that has the centre point of the centroid * as reference point. Table 1 shows the data for a simple biconvex lens. To each table there is a figure that shows the lens or lens system´s appearance.
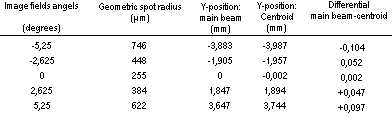
Table 1. Simple biconvex lens of BK7 glass.
 Figure, table 1.
Figure, table 1.Let us now investigate what happens if we allow the optical program to optimise the form of the lens. The result appears from the figure and table 2 below.
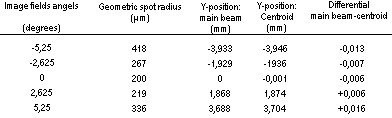
Table 2. Simple BK7 lens with optimised form.
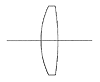 Figure, table 2.
Figure, table 2.From table 2 it is clear that both the spot radius and the distortion have been reduced considerably when we had the computer optimise the form of the lens.
We shall now investigate what happens if we replace the glass that in the first two cases were BK7 with SFL6 and the same time optimise the form of the lens. The result appears from the figure and table 3 below.
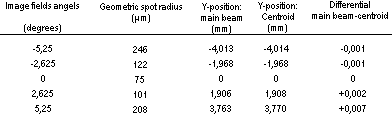
Table 3. Simple SFL6 with optimised form.
 Figure, table 3.
Figure, table 3.From table 3 it appears that both the spot radius and the distortion were further reduced when we used a high refractive index glass and had the computer optimise the form of the lens.
In order to reduce the distortion and further enhance the image definition we have to make use of a composite lens sytem.
Lens system
A lens system comprising two lenses is called a duplex. If there is an air gap between the lenses the duplex is termed separated and if the lenses are stuck together the duplex is called cemented. A duplex that is corrected so that the image location for two wawe-lengths coincide and - at the same time - meet the aplanatic requirements ** is called achromatic ***.
The next system that we should examine is therefore a separated duplex. The result appears from the figure and table 4 below.
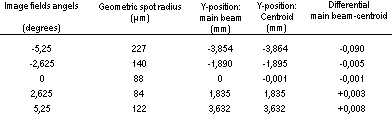
Table 4. Separated duplex comprising 2 SFL6 lenses.
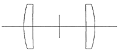 Figure, table 4.
Figure, table 4.It appears from the table that the distortion is greater but the spot radii are somewhat smaller than for the optimised SFL6-lens.
* For explanation of the term centroid, see section 10 ** A lens meets the aplanatic requirement if it is corrected for spherical aberration and meets Abbe´s sinus requirements. *** It was the English lawyer Chester M. Hall who worked out an achromatic lens for the first time in 1729.
We shall now test a cemented duplex that consists of two cemented lenses of two different optical glass types i.e. in principle an achromatic lens system. Since a triangulation probe operates most frequently on a single wave-length this means that we do not need to think of carrying out colour correction of the achromatic lens system when having the computer optimise it. The result appears from figure and table 5 below.
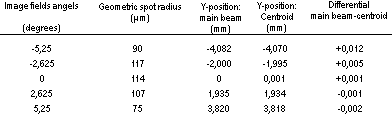
Table 5. Cemented achromatic lens comprising glass types BK10 and SF5.
 Figure, table 5.
Figure, table 5.From table 5 it appears that the distortion is relatively small but the different spot radii are still very large.
Cooke triplet
We shall now examine a three-lens system - to be more precise a so-called Cooke triplet. The Cooke triplet is by no means the only conceivable three-lens lens system. There are in fact some thirty or so different three-lens systems described in the technical literature relating to optics. I have only chosen it as being a very commonly occuring lens. The Cooke triplet was designed in 1893 by Dennis Taylor who was employed as chief engineer by Cooke of York. Since this company was not interested in manufacturing photographic lenses Taylor arranged for another optical company to produce the lens but out of respect for Taylor´s employer the lens has frequently been called a Cooke triplet ever since. The Cooke triplet is the simplest lens system that allows - at the same time - the correction of third order aberrations but this does not meanthat the aberrations can be reduced right down to zero. A Cooke triplet comprises a negativ flint glass lens in the centre with a crown glass lens on each side. The aperture is most frequently placed as in figure 6.
The result for a Cooke triplet appears in the figure and from the table 6 below.
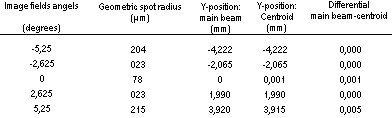
Table 6. Cooke triplet comprising SK16, F2 and SK16 lenses.
 Figure, table 6.
Figure, table 6.It appears from table 6 that the distortion is low except at the field angle + 5,25° but it is also evident that the Cooke triplet is overstrained due to the requirement that the entrance aperture shall be 15 mm.
Let us therefore reduce the entrance aperture to 10 mm and examine what happens. The result appears from the figure and table 7 below.
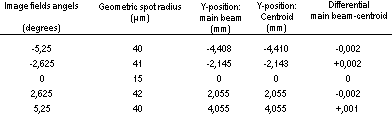
Table 7. The same Cookie triplet as in table 6 but the solution is optimised for an entrance apertur of 10 mm.
 Figure, table 7.
Figure, table 7.We now see that both the spot radii and the distortion have been considerably reduced. We now have spot diameters of the magnitude of 80 µm and the distortion has been reduced to approx. 2 µm.
If we wish to retain the requirement that the entrance aperture shall be 15 mm we must introduce a lens system that comprises at least 4 lenses.
In section 12 of the PSDschool we will investigate a few other lens systems and also give some general considerations regarding mechanics.
|
« home